Hours of entertainment here!
I'm glad that at least one other person feels that way! I found the most challenging part, though I did not pose it to the readership, was to find the minimum-error sequence for board-closing roll sets that lack a perfect-play solution. Perhaps the most interesting such roll set is 33 44 66 66. First, a digression...
Decades ago, I discovered it was possible to make a six-point prime from the 7pt to 2pt in three doublet rolls (along with many other oddities, such as repeating the original position in four doublet rolls, anything my warped mind could conjure). Much later, I heard that Bill Davis had discovered the same prime-making sequence (probably before I did), and had even created a clever story around it, entitled The Great Prime Problem (originally printed in Gammon Magazine in 1980).
The reason this problem is tricky is that practical backgammon moves aren't used in the making of the prime -- no doublet is moved in two convenient pairs. The experience is more like piecing together a jigsaw puzzle. Contrast this with making a less-deep prime from the 8pt to 3pt with 53P + 22N + 66O, or from the 9pt to 4pt with 31P + 22N + 44D -- as discussed above the second-to-last diagram of this post -- plus there are additional options if all three rolls are doublets. Those are all relatively easy combinations to find.
Below are three diagrams. To best follow my explanation, please widen your window until you can see all three diagrams side-by-side-by-side.
To make a six-point prime from the 7pt to 2pt, the only three-roll set is 44 + 33 + 66 (though they can be played in any of the six possible orders). The 44 is always played exactly as shown in the first diagram.
Likewise, the 33 and 66 are played exactly as in the second and third diagrams, with one roll portion excepted. If the 33 is rolled first, one of the 6s will be played 10/4 instead of 13/7. If the 66 is rolled first, one of the 3s will be played 7/4 instead of 13/10. In other words, one of the midpoint checkers will arrive at the 4pt either by 13/10/4 or 13/7/4; all other move portions are fixed.
   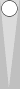  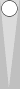 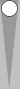    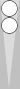                        |
| ||||
| XGID=-b----------d----b-daa-a--:0:0:1:00:0:0:0:3:10 | |||||
White played 44J_ (13/5 8/4 6/2) | |||||
      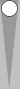    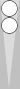  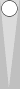                      |
| ||||
| XGID=-b----------d--a-b-ca-b---:0:0:1:00:0:0:0:3:10 | |||||
White played 33I_ (13/10 8/5 6/3(2)) | |||||
   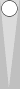       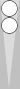                     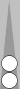   |
| ||||
| XGID=-b----------b----bce---a--:0:0:1:00:0:0:0:3:10 | |||||
White played 66O. (13/7(3) 8/2) | |||||
When combined, the three moves represented above produce...
   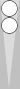  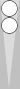                             |
| ||||
| XGID=-b----------a-----bbbbbb--:0:0:1:00:0:0:0:3:10 | |||||
Six-point prime from 7pt to 2pt | |||||
From here, either of two rolls, 33 or 66, close White's board. Therefore, if it were stipulated that White is to make this six-point prime and THEN close her board, only 2 possible sets of four rolls could accomplish the task: 33 44 66 (in any of the six possible roll orders) plus either (a) 33 or (b) 66.
Of course, I did not make that stipulation in my Getting Closed Out puzzle. Instead of a mere 2 possible roll sets to close the board, there are (at least) 19 -- the ones I enumerated here. The one listed there as #11 is the same as (a) in the paragraph above, and #19 is the same as (b).
Given that there are an odd number of checkers on the 8pt and 6pt, it is never possible for all four doublets to be entirely played in pairs. Still, a second 33 grants a lot more flexibility. For example, for the #11 sequence, 52S-33A-31U-66P-F-33H-2-44A (with White's moves in gray typeface), both halves of White's first two rolls are played in pairs, and she leaves a blot in her board only once in the sequence (with 33H = 13/10 13/4*).
The other roll set, 33 44 66 66, is considerably more problematic. This is the only one of the 19 roll sets that forces White to employ the convoluted "mesh" required to solve the The Great Prime Problem. Granted, White has eight 6s, but she must still play four as shown earlier (13/7(3) 8/2). With two other 6s she must play 13/1(2), and although she can play her remaining two 6s in any legal way (13/1, 13/7 24/18, or 24/18(2), or even 24/12 if Blue somehow breaks his midpoint), none of that offers a meaningful way to vary from the mesh.
Out of the 19 board-closing roll sets, I was unable to find perfect-play solutions for 7 of them. Rather than leave it at that, I looked for minimum-error sequences. Initially, I just tried for the fewest number of errors, and once I whittled each of the seven down to one error, I aimed to minimize the size of that error. Finally, in addition, I looked for the smallest total error size for each (a more challenging process, and it is those sequences I ended up posting).
The toughest roll set to solve for, both to minimize the single-error size and total-error size, was the aforementioned 33 44 66 66. I'll show both solutions, admitting at the outset that I haven't searched exhaustively -- there may be something even better.
First, the sequence with the smallest single error:
                                  |
| ||||
| XGID=-----ADbC---cF---cbe--A---:0:0:-1:44:0:0:0:3:10 | |||||
Blue opened with 65R, | |||||
Blue has played two moves: 65R (24/13) and 21W (24/22 6/5), straightforward enough. Meanwhile, White has played the powerful 66B (24/18(2) 13/7(2)), and her next roll is 44. Can you guess how she will play it?
   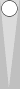 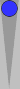 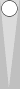 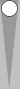                            |
| ||||
| XGID=-----ADbC---bF---bbdaaAa--:0:0:1:53:0:0:0:3:10 | |||||
White played 44J_, Blue rolls 53 | |||||
It may seem strange that of the three mesh-plays I diagrammed at the beginning of this post, I would choose the worst-looking one (the 44J_ triple-slot) to be White's error. The problem is: if I peg the less-horrendous 33I_ or 66O_ as the error (for either White's first or second turn), I still can't quite turn a subsequent 44J_ into the best play. By contrast, it IS possible to find a friendly 66 + 33 combination after 44J_ is on the board. In short, it is necessary to do the best we can with the ugliest move.
Note that Blue's play to this point has aimed to minimize White's equity loss in triple-slotting with 44. Blue has leapfrogged over White 2pt so that he'll only have a double shot at White's blots, and if he does hit then his own slotted 5pt might get hit back. Furthermore, Blue has escaped his other back checker (otherwise he would either have more shots, or he would be anchored -- in which case he could no longer be induced to run).
Even with all that, White's .655 error is a painful blow (best is C (18/14(2) 7/3*(2)), but the remainder of play in this sequence will be perfect.
What roll can we now assign Blue? We can't permit him to hit or run. It must be a roll that is blocked: 54 53 43 55 44 or 33.
It happens that the only roll that works for Blue is 53 (I'll clarify in a moment), which he plays in the obvious way...
                                  |
| ||||
| XGID=-----BDbC---bE---bbdaaAa--:0:0:-1:33:0:0:0:3:10 | |||||
Blue played 53P, White rolls 33 | |||||
Note that if, instead of the carefully selected 53P (13/5), Blue had played 54D, his board would be unimproved and White would cube (cooking the sequence). On the other hand, if Blue had played 43O (13/9 8/5), 33O_ (13/10(3) 8/5), 44O_ (13/9(3) 9/5) or 55P (13/3(2)), White's best 33 play will be to cover her 2pt with I_ (7/4 6/3*(2) 5/2), which makes it impossible to close her board in one more roll.
In short, Blue's only roll to keep the sequence alive is the needle-threading 53, and now White rolls the anticipated 33...
                                  |
| ||||
| XGID=-----BDbC---bE---aabbbba-A:0:0:-1:66:0:0:0:3:10 | |||||
White played 33A, Blue Fans, White rolls 66 | |||||
White has been happily "manipulated" into the aggressive play with 33, and she can therefore close her board with 66.
For reference, the runner-up single-error sequence is: 65R-66B-61&-44J_55P-66O.F-33A, where 44J_ is an error of .661. If White plays 44J_ as early as on her first turn, her error is smallest (.695) in 63S-44J_52S-66B-55o.-66O.F-33A
Finding the sequence with the smallest total error size (without regard to the number of errors) is somewhat trickier; there are more tradeoffs to consider. Ultimately, I decided the most bang for the buck could be gained by minimizing White's double 3s error, and supporting that with a couple of measured sacrifices.
My basic plan is to get White checkers to her 7pt, put Blue blots on White's 5pt, 4pt and 3pt, and let her attack with 33. That way, when she "slots" her two highest points, she'll actually be hitting there, while the diversion of pointing on the 3pt will greatly reduce the error of not covering the other two blots (after all, she only has four 3s).
To get a third Blue checker back, it must be hit on the near side, obviously. As a 6 is the only number White can spare for a back checker (and White needs 6s to put checkers on her own bar point anyway), the 7pt is the point Blue must SLOT. And, on the same opening roll, he must SPLIT to the 22pt, 21pt or 20pt, so that on his second turn he will be able to advance all three back checkers (the two originals plus the one hit on his 7pt) to the three different points high in White's board.
There are six possible ways to split and slot in the manner described. (Split occurs with 2, 3 or 4, and the 7pt-slot occurs with a 6 or 1.) None of them are the best backgammon play, of course, but the smallest error is with an opening 63. Nevertheless, I paid an additional .010 by assigning Blue a roll of 64 (I'll explain why in a moment).
                                  |
| ||||
| XGID=------EbC---cD---cbeA---AA:0:0:1:33:0:0:0:3:10 | |||||
Blue played 64Z, White played 66B, Blue rolls 33 | |||||
Blue opened with 64Z, an error of .089. This may seem like a big sacrifice, but if we can hold the largest error to a double- or triple-whopper, it will be a good investment.
If Blue starts the game by split and slotting instead with 63, 31, 62 or 21, then (after White's 66B), he can come off the roof with whichever of 52U (bar/20 24/22) or 53U (bar/20 24/21) sets up the triple blot. However, White would have a cube in of those situations, and they are thus disqualified. (Of the six split-and-slot openers, then, I was left with 64Z and 41B (24/20 8/7). The latter is an error of .175 and doesn't make up the difference later in the sequence, so I went with 64Z.)
The virtue of 64Z-66B-33 (see diagramm) is that after advancing his back checkers, Blue has two leftover 3s with which he can strengthen his forward position enough to stave off the cube. Unfortunately, her best plays with 33 don't move two back checkers, which means another sacrifice is necessary. So, bar/22 24/21 it is; then the plausible ways to play two 3s on the near side (i.e., strong enough not to get cubed) are 6/3(2), 13/10(2) and 8/5(2), which are respective errors of .024, .040 and .094.
I checked XGR++ to see how big an error White's assigned 33A (8/5* 7/4* 6/3*(2)) response will be in each case. The answer is .323, .276 and .370, respectively, and that tells us everything we need to know. We should go with Blue's middle play (the one that includes 13/10(2)). That way, the extra .016 we invest saves us .047 on White's error in response. To wit...
                                  |
| ||||
| XGID=------EbC-B-cB---cbeAAA---:0:0:-1:33:0:0:0:3:10 | |||||
Blue played 33B, White rolls 33 | |||||
As discussed, Blue played 33B (bar/22 24/21 13/10(2)), and we have achieved the setup we want for White's 33. In competition, White should point on two of the blots, the best of those options being A (8/5*(2) 6/3*(2)). However, that leaves no way to close her board in two more rolls. Therefore, she must play...
                                  |
| ||||
| XGID=------EbC-B-cB---bacaabA-B:0:0:-1:44:0:0:0:3:10 | |||||
White played 33A, Blue entered with a 2, White rolls 44 | |||||
White played 33A (8/5* 7/4* 6/3*(2)), an error of .276. Perhaps it is easier to see now why Blue was assigned 13/10(2) with those two 3s. If he had made an inside point with 8/5(2) or 6/3(2), the cost of White getting hit on her 5pt or 4pt would be even greater.
Take a moment to scroll back and look at the third diagram of this post, showing White's bizarre 44 triple-slot play. Now notice how well that same play fits the current diagram (above this text) -- it's the best move by far.
                                  |
| ||||
| XGID=------EbC-B-bB---aabbbba-C:0:0:-1:66:0:0:0:3:10 | |||||
White played 44J_, Blue Fans, White rolls 66 | |||||
White was too good to double prior to her rolls of 44 and 66. I trust you can see how she closes her board with 66.
Nack