                        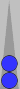   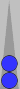 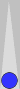      |
| ||||
| XGID=---aB-B-BA--cDb--d-e--B-AA:0:0:1:43:0:0:2:0:10 | |||||
Blue owns 8pt: [P @16] "<=10 | |||||
| 1. | Rollout1 | Bar/22 13/9 | eq: -0.227 | |||
| ||||||
| 2. | Rollout1 | Bar/21 24/21 | eq: -0.242 (-0.016) | |||
| ||||||
| 1 10368 Games rolled with Variance Reduction. Dice Seed: 15090110 Moves: 3-ply, cube decisions: XG Roller | ||||||
  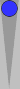  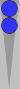                  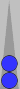  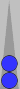          |
| ||||
| XGID=---aB-BB-A--cDb--d-e--B-AA:0:0:1:43:0:0:3:0:10 | |||||
Blue owns 7pt: [@ P10] "<=10 | |||||
| 1. | Rollout1 | Bar/21 24/21 | eq: -0.297 | |||
| ||||||
| 2. | Rollout1 | Bar/22 13/9 | eq: -0.307 (-0.010) | |||
| ||||||
| 1 10368 Games rolled with Variance Reduction. Dice Seed: 55565956 Moves: 3-ply, cube decisions: XG Roller | ||||||
For the first (i.e., lefthand) position above, John's rollout is [P @30], Colin's rollout is [P @18], and my rollout (above) is [P @16]. Combining John's 3k trials with Colin's 15k and my 10k yields a 30176-trial result of [P @19].
A comparison of this (combined) margin of .019 to that of the second (i.e., righthand) position above, which has the other (anchoring) play winning by .010, sums to a difference in margin of .029. Why is P that much stronger in the first position than in the second position?
As I was posting, I noticed that Colin mentioned 65 being a key number. Indeed, the spotlighting of 65 was precisely the reason I had created the variant position! The race and other strategic factors alone should not point to P being better in the first position. A proper accounting necessarily includes the blocking of 65. Otherwise one is essentially left with the superiority of anchoring as in the second position. [There is a partially offsetting effect for the roll of 51, which I'll get to in a minute.]
Suppose Blue covers the 9pt with P. In the second position, White's equity after cleanly escaping with 22/11 is .544 better (granted, XGR++ evals are not perfect and the methodology is rough/incomplete) than her least unattractive near-side option of 13/2. Dividing .544 by 18 (because 65 is rolled 1/18 of the time) comes to .030, which is very close to the number summed up two paragraphs ago. Based on that, Blue's blocking of 65 (with P) in the FIRST position basically accounts for the entire P/@ difference between the two positions. Without it, anchoring would be the better play.
The effect of 51 is a bit more complicated. In the 8pt position, against either move White plays 8/2, though Blue's P (by virtue of retaining 24/23*) net gains .087. In the 7pt position, White plays 22/17 6/5 or 16* (the biggie), where P net gains .267. The net net is that P (vs @) gains .180 more in the 7pt position, and dividing that by 18 is .010.
Subtracting .010 (the effect of 51) from the thrice-as-large .030 (the effect of 65) yields .020. This is .009 less than the rollout difference of .029 noted in my second paragraph. That .009 might be reconciled by errors in the XGR++ evaluations (corrected in the rollouts), corner-cutting and/or other minor adjustments.
John said: "If you cover the 9-point in Nack's altered position, the only bad roll for White is 51. In my original position, covering the 9 makes 65,53, and 51 all weak numbers for White. That's probably enough to swing the decision to making the 2nd anchor in Nack's position."
John is a top player in part because he is good at spotting/creating bad numbers for his opponents. He found 65 here. He appears to have simply cancelled out the 51, though as noted (in comparing the two positions for P/@ differences) it actually erases 1/3 of the 65 effect (but at least he saw and mentioned it). IMO, the effect of 53 is negligible, because in the first position it is already blocked either way; and in the second position, it runs out either way. Still, John came to the right conclusion.
Below is a bonus pair of positions. In the first (lefthand) position, P (Point, bar/22 13/9) beats @ (anchor, bar/21 24/21) by .027. In the second (right-hand) position, @ beats P by .036. How do you explain this huge P/@ swing of .063? Perhaps with a fairy tale? Following the rollouts is some analysis.
                     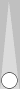   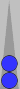  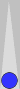 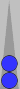       |
| ||||
| XGID=---a-BBAB--BcBb--d-e--B-AA:0:0:1:43:0:0:3:0:10 | |||||
Blue owns 8pt: [P @27] "<=5 | |||||
| 1. | Rollout1 | Bar/22 11/7 | eq: -0.107 | |||
| ||||||
| 2. | Rollout1 | Bar/21 24/21 | eq: -0.134 (-0.027) | |||
| ||||||
| 1 5184 Games rolled with Variance Reduction. Dice Seed: 38402675 Moves: 3-ply, cube decisions: XG Roller | ||||||
  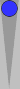  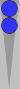          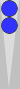       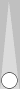             |
| ||||
| XGID=---a-BBA-B-BcBb--d-e--B-AA:0:0:1:43:0:0:3:0:10 | |||||
Blue owns 9pt: [@ P36] "<=5 | |||||
| 1. | Rollout1 | Bar/21 24/21 | eq: -0.110 | |||
| ||||||
| 2. | Rollout1 | Bar/22 11/7 | eq: -0.145 (-0.036) | |||
| ||||||
| 1 5184 Games rolled with Variance Reduction. Dice Seed: 7847218 Moves: 3-ply, cube decisions: XG Roller | ||||||
In the same vein as 65 in the earlier position pair, 54 is a key number affecting the pair immediately above. According to XGR++ evals, in the first position, playing P allows Blue to end up .417 better off when White has to play 13/8 6/2 instead of escaping to the midpoint. In the second position, Blue loses .015 (because after @ the vacant 8pt allows White to run with 22/17/13 without hitting!). In short, the roll of 54 explains (.417 – .015) / 18 = .022 of the .063 swing (that we aim to reconcile).
The other important roll is 53. In the second position (but not the first), covering the bar point leaves a blot on the 11pt, letting White hit there, which costs .432. In the first position, 13/10 6/1* after P does better than 13/5 after @, which refunds .043. Netting those, the roll of 53 explains another (.432 – .043) / 18 = .022 of the aforementioned .063 swing.
I'll spare you the details, but the roll of 62, minus the rolls of 42 and 41, net another .002. So far, that accounts for (.022 + .022 + .002) = .046. The remaining .017 seems too large to explain away by XGR++ misevaluations or variance. I hypothesize that most of that remainder has to do with the additional value of filling in the inside point of the prime (covering the 7pt) when it is consecutive with the 8pt (compared to being non-consecutive with the 9pt).
Finally, note that some pairs of points (9pt + 8pt, and 8pt + 7pt) typically work better together in containing a 3pt checker (or two checkers there, in some positions) than others. The 9pt + 8pt prevent an escape with 65. The 8pt + 7pt prevent an escape with 54. By contrast, the 9pt + 7pt seem to block 64 but actually the midpoint already blocks it -- though double 5s may erase half of that reason. (In other words, in blocking the 3pt, the 13pt + 9pt + 7pt combination is non-optimal.) Likewise, for example, the 10pt + 7pt and 9pt + 8pt pairs can be a bit less efficient than other pairs of points in the containment of 4pt checker(s).
Nack